Dr. Claudia Zimmermann

Thermally driven flows are described as a turbulent compressible Rayleigh-B´enard problem. For the numerical discretisation of the Large-Eddy-Simulation the flow is separated in large and small scales, the so-called sub-grid scales. The large scales are solved directly on the discretisation grid, while the sub-grid scales are modelled with an applicable turbulence model.

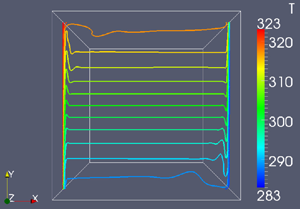
A rectangular, air-filled container is chosen as test case. The walls are smooth and the vertical ones are heated homogeneously with a constant temperature difference. For the lateral walls different boundary conditions are investigated. Due to a non-slip-condition the velocity field at the walls is zero in all cases. The Rayleigh-number Ra=1.58e9 and the Prandtl-number Pr=0.71 are always constant. The vertical positioning of the heated plates parallel to the direction of gravity effects a steady state flow. Two recirculations zones in the vincinity of the temperature-controlled walls can be seen. A variation of the thermal boundary layer becomes apparent. The profiles of the temperature and the vertical velocity between the temperatured walls are plotted against the experimental data.

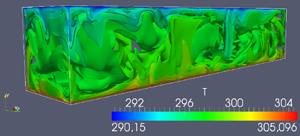
The thermal driven flow in the container is effected by the decreasing density and the resulting pressure gradient in direction of gravity. The intensity of the turbulence increases with the shear flow interaction of hot lift streams and cold sinking streams. Singular hot gas plugs break through the cool sinking flows. This unsteady behaviour dominates the vertical heat flux. This is illustrated by the instantaneous temperature iso-surfaces for 1.92e8. The plots of the mean horizontal and vertical velocity of the xy-midplane at one time step show the typical convection cells which are developed between the temperature-controlled walls.