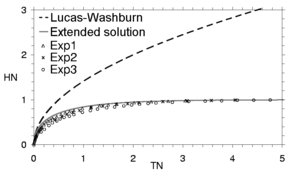
An analytic solution for the capillary rise of liquids in a cylindrical tube or a porous medium is derived in terms of height h as a function of time t. The implicit t(h) solution by Washburn is the basis for these calculations and the Lambert W function is used for its mathematical rearrangement. The original equation is derived out of the 1D momentum conservation equation and features viscous and gravity terms. Thus the h(t) solution, as it includes the gravity term (hydrostatic pressure), enables the calculation of the liquid rise behavior for longer times than the classical Lucas-Washburn equation. Based on the new equation several parameters like the steady state time and the validity of the Lucas-Washburn equation can be examined. The results are also discussed in dimensionless form.

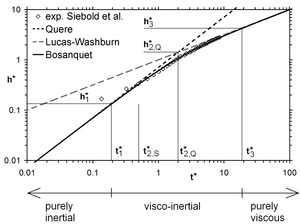
The initial moments of capillary rise of liquids in a tube is investigated. In this period both inertia and viscous flow losses balance the pressure generated by the meniscus curvature (capillary pressure). It is known that the very first stage is purely dominated by inertial forces, where subsequently the influence of viscosity increases (visco-inertial flow). Finally the effect of inertia vanishes and the flow becomes purely viscous. The times and meniscus heights at which the transition between the time periods occur are derived. This is done in an attempt to provide a method to determine a priori which terms of the momentum balance are relevant for a given problem. Analytic solutions known from previous literature are discussed and the time intervals of their validity compared. The predicted transition times and the calculated heights show good agreement with experimental results from literature. The results are also discussed in dimensionless form and the limitations of the calculations are pointed out.

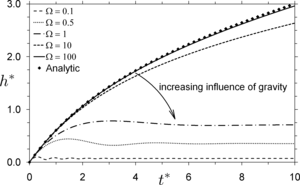
To obtain dimensionless scalings the different methods for capillary rise of liquids in a tube or a porous medium are discussed. A systematic approach is taken, and the possible options are derived by means of the Buckingham Pi theorem. It is found that three forces (inertial, viscous and hydrostatic forces) can be used to obtain three different scaling sets, each consisting of two dimensionless variables and one dimensionless basic parameter. From a general point of view the three scaling options are all equivalent and valid for describing the problem of capillary rise. Contrary to this for certain cases (depending on the time scale and the dominant forces) one of the options can be favorable. Individually the different scalings have been discussed and used in literature previously, however, we intend to discuss the three different sets systematically and try to evaluate when which scaling is most useful. Furthermore previous analytic solutions are discussed and their ranges of applicability when compared to numerical solutions of the differential equation of motion (momentum balance) are evaluated.