numerical investigations
numerical simulation of surface reorientation of free capillary interfaces upon step reduction in gravity
introduction
For fluid systems with free interfaces, the competition between gravitational forces and surface tension forces is usually expressed through the Bond number Bo, where
|
with ρ, a, R and σ denoting liquid density, accelaration due to gravity or another force, characteristic geometrical length and fluid intefacial tension. In cases where Bo << 1, the effects of gravity are small in comparison to those of surface tension and capillary dominated systems result. A reduction of gravity reduces the pressure in the fluid. By unloading the hydrostatic pressure, interface oscillations are started and interfacial forces are no longer masked by earth gravity. The fluid flow from an essentialy flat surface configuration towards its low gravity equilibrium shape, one generally of constant curvature meeting the container wall at the contact angle ϒstat of the system (Fig.1)
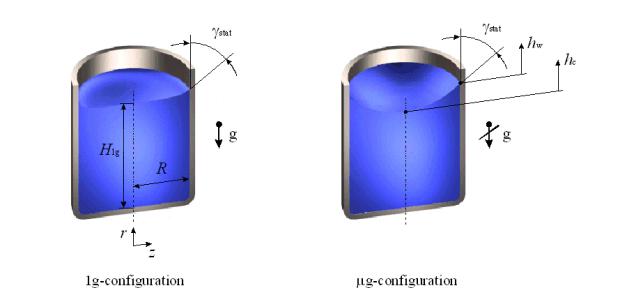
Dependent on the damping of the system, an overshoot can result and oscillation about the equlibrium surface shape occurs until damped. An important dimensionless number, somewhat analogous to the damping ratio in the spring mass-damper system, is the Ohnesorge number Oh, where
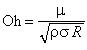 |
with μ denoting the fluid dynamic viscosity.
numerical model
The numerical simulations were performed with the finite element code FIDAP (version 8.6.1). The numerical results are compared with experiments which were carried out at the drop tower in Bremen to investigate the reorientation behavior of the liquid interface, which is assumed to be axisymmetric. The computational region is reduced to the half plane of the vertical section alng the symmetry axis. The fluid is assumed to be incompressible, isotherm and Newtonian with a passive overlaying gas phase. The intention to describe the fluid motion mathematically encounter the fundamental difficulty modelling the moving contact-line problem. The classical formulation of the problem with the no-slip boundary condition on a solid surface give rise to a non-integrable singularity of the shear stress. In addition the dynamic contact angle value ϒ dyn cannot be found and must be prescribed.The boundary conditions for the numerical simulated problem of surface reorientation comprise a boundary condition for the dynamic contact angle and a slip-condition. We use the Navier slip condition for the node who represent the contact line. The numerical model for the dynamic contact angle includes the dependence on the contact line velocity and considers the the contact angle hysteresis which strongly affect the reoriention process. The model deduced from the relation from Jiang (1979). We adjusted the constants for a better agreement with the experimental data (Gerstmann 2003). At the wall peaks of the contact line hiytory the velociyt goes to zero and the contact angle hysteresis occurs.
numerical results
A typical behavior of the contact line and the center point history is shown in Fig. 2 in comparison with the numerical simulation calculated with the developed dynamic contact angle boundary condition.
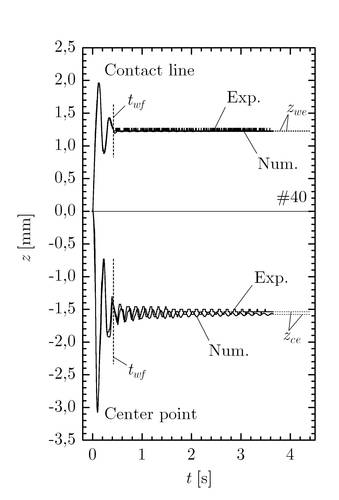
The center point is the surface point at the symmetry axis. After a few oscillations, at the time twf, the contact line is pinned and the damping of the center point oscillation decreases. The calculated contact line velocity and dynamic contact angle display the basic dependence of the dynamic contact angle on the contact line velocity. In general we find very good agreement between the numerical and experimental data. The wall and center peak, the pinning of the contact line, damping and frequency coincide.


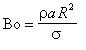
 "
"